Standard ottici
Libera traduzione di Giorgia Giabardo dal sito Oldham Optical
Vi sarà capitato di constatare che la qualità della superficie di uno specchio può essere definita con varie unità di misura. Fra le più comuni c’è il Peak to Valley (PV) sulla superficie; Peak to Valley (PV) sul fronte d’onda, (o nel punto focale); RMS levigatezza o fattore Strehl.
Per poter fornire una spiegazione più approfondita servirebbe un intero libro di ottica, nel breve spazio del nostro sito possiamo però dare un’idea in termini pratici di quale significato hanno queste misure e quali sono i valori “buoni” cui mirare.
Avrete notato che quando si cita il PV o l’RMS la prima cosa da sapere è se si sta misurando la superficie o il fronte d’onda, questo è importante poiché il valore di uno e` il doppio dell’altro
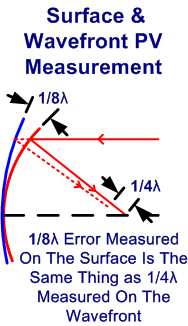
Un buono standard per uno specchio, secondo molti testi di astronomia, è un errore PV 1/8 lambda misurato sulla superficie dello specchio, – che poi sarebbe uguale ad un errore 1/4 lambda PV misurato sul fronte d’onda. Questo riferimento, originariamente proposto da Lord Rayleigh, è noto come “Tolleranza Rayleigh”.
Il corrispondente errore RMS sul fronte d’onda per questi valori di PV è di circa 1/15lambda mentre il rispettivo valore Strehl e` di circa 0.82.
Tutti questi valori probabilmente vi staranno già mandando in confusione!!! – Quindi sarà meglio chiarire cosa significano in pratica un errore PV 1/4lambda sul fronte d’onda e gli altri valori e, soprattutto, se il valore di 1/4lambda è davvero un buon valore di riferimento.
Il punto di partenza
Purtroppo nel mondo reale e`impossibile realizzare uno specchio assolutamente perfetto. Tutti gli specchi “reali” hanno sempre dei difetti di qualche sorta.
Tuttavia, supponiamo che un produttore di specchi riesca a fare uno specchio assolutamente perfetto. Tale specchio avrebbe una curva parabolica esattamente corretta, non avrebbe alcun difetto o rugosità superficiale, perciò vi aspettereste che focalizzasse tutta la luce proveniente da una stella in un singolo punto infinitamente piccolo, vero?
Spiacenti! – Restereste delusi!
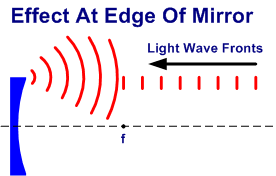
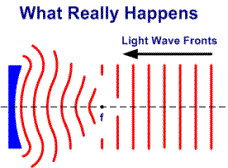
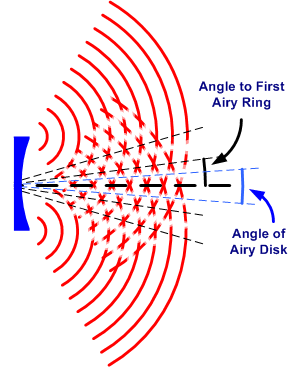
La spiegazione di ciò che accade è molto semplice ed è dovuta alla natura della luce. Lo specchio la focalizza in un disco dalle dimensioni definite. Anziché focalizzare la luce nel singolo punto infinitamente piccolo come vi sareste aspettati. All’esterno di tale disco centrale, ci sono poi anche alcuni anelli sfocati, e l’insieme del disco e degli anelli è semplicemente chiamato “Disco di Airy” dal nome della persona che per primo lo analizzò dal punto di vista matematico. Nessuno specchio, perfetto o no, riesce focalizzare la luce in un punto più piccolo di tale disco e, ogni ulteriore difetto dello specchio, non fa altro che ingrandire il disco stesso.
La dimensione del disco di Airy dipende dalla lunghezza d’onda della luce e dal rapporto focale dello specchio. La formula è quella che segue nella tabella:-
| D = 2.43932 x lambda x Rapporto Focale D = Diametro del disco di Airy in mm lambda = Lunghezza d’onda in mm (es. 546nM = 0.000546mm)La tabella a fianco da` valori per 546nM |
Rapporto focale |
Dimensione Disco di Airy mm |
| F/3.5 | 0.00466 | |
| F/4 | 0.00533 | |
| F/5 | 0.00666 | |
| F/6 | 0.00799 | |
| F/8 | 0.01065 | |
| F/10 | 0.0133 | |
| F/15 | 0.020 | |
| F/20 | 0.0266 |
Perciò, se anche un costruttore realizzasse uno specchio perfetto, – questo non metterebbe comunque a fuoco in modo perfetto.
Maggiori informazioni sul Disco di Airy – e perche` non si puo` evitare Specchi a Diffrazione Limitata
Qualsiasi difetto dello specchio, rugosità superficiale o deviazione da una forma perfettamente parabolica, provocherà un’ulteriore sfocatura che andrà ad aggiungersi a quella dovuta al disco di Airy.
Tuttavia, se il difetto è piccolo e la sfocatura che ne deriva è inferiore al diametro del disco di Airy, allora, la difettosità dello specchio ha un impatto molto marginale. Vengono definiti specchi a ”Diffrazione Limitata” tutti quegli specchi in cui i difetti sono così piccoli da provocare una sfocatura inferiore a quella dovuta al disco di Airy.
C’e` una leggera riserva in merito alla possibilità di osservare la luna o i pianeti di cui discuteremo più avanti ma, se usate il vostro telescopio a diffrazione limitata per vedere fonti puntiformi, allora esso avrà prestazioni altrettanto valide di quelle di uno specchio perfetto.
Ne consegue che, per un produttore di specchi, professionale o amatoriale che sia, un buon obiettivo è quello di produrre uno “Specchio a Diffrazione Limitata”.
Pur essendo possibile produrre uno specchio ancora migliore di uno a diffrazione limitata, di fatto, oltre a questo limite, il miglioramento della performance è minimo in rapporto al lavoro supplementare, questo perché il disco di Airy rimane l’errore dominante che non può essere rimosso.
“Valori” a diffrazione limitata Non c’è unanimità nel definire la soglia oltre alla quale uno specchio può essere considerato a diffrazione limitata ed il dibattito e` sempre aperto.
Sono stati proposti vari limiti, fra i quali anche quello chiamato “Tolleranza Rayleigh”. Anche Oldham Optical propone una propria interpretazione e, qui di seguito, illustreremo ciò che otterrete se acquisterete uno specchio a “Diffrazione Limitata” da noi.
Esiste un programma ottico professionale con cui è possibile riprodurre vari difetti su specchi di misure diverse e determinare il limite dove la sfocatura provocata dall’errore dello specchio ha la stessa dimensione del Disco di Airy.
| Limiti di diffrazione di specchi di varie dimensioni, misurati con varie unita` di misura | ||||
| Specchi | Dimensione mm del disco di Airy |
Peak to Valley sul fronte d’onda lambda |
RMS Levigatezza superficiale |
Rapporto Strehl |
| Specchio perfetto | Vedi sotto | 0 | 0 | 1 |
| 158mm F/7.7 | 0.010 | 0.154 | 0.044 | 0.925 |
| 158mm F/4.8 | 0.0064 | 0.156 | 0.044 | 0.923 |
| 222mm F/4.5 | 0.0060 | 0.155 | 0.044 | 0.924 |
| 304mm F/4.3 | 0.0057 | 0.156 | 0.045 | 0.923 |
| 406mm F/5 | 0.0066 | 0.155 | 0.044 | 0.924 |
| 495mm F/4.1 | 0.00546 | 0.150 | 0.043 | 0.929 |
| 610mm F/3.8 | 0.0050 | 0.152 | 0.043 | 0.927 |
| 762mm F/4.5 | 0.0060 | 0.152 | 0.043 | 0.927 |
La tabella precedente è stata realizzata utilizzando “ZEMAX”, un programma ottico professionale per la tracciatura di raggi. I dati che essa fornisce rappresentano il valore dell’errore dello specchio che provoca una sfocatura dello stesso diametro di quella del disco di Airy. In cima alla tabella è stato inserito come riferimento uno specchio perfetto, in modo da mostrarne – qualora fosse possible produrne uno – i relativi valori.
Per gli esperti che hanno accesso a ZEMAX, è bene chiarire che i valori sono stati ottenuti partendo da uno specchio parabolico perfetto dal diametro e rapporto focale noti, per poi deformarlo alterando la costante conica ma, al tempo stesso, cercando di ottimizzare fino a quando il punto risultante sia contenuto all’interno del disco di Airy. Una volta ottenuta questa condizione, – l’errore di fronte d’onda e Strehl vengono cercati ri-ottimizzando verso il minimo errore di fronte d’onda (questo metodo assume che la superficie dello specchio sia perfettamente liscia). Infine, la lunghezza d’onda della luce utilizzata è 546nM.
C’è una leggera discrepanza nei valori, dovuta al giudizio umano, esattamente quando lo specchio raggiunge il valore necessario, è comunque chiaro che uno specchio deve essere uguale o migliore di PV 0.150lambda, (errore di fronte d’onda di circa 1/6.6lambda) o RMS 0.043lambda, (circa RMS 1/25lambda), o Strehl 0.93. Ne consegue che, se si utilizza il criterio secondo il quale l’errore dello specchio non deve provocare una sfocatura maggiore del disco di Airy, qualsiasi specchio il cui un errore di fronte d’onda è inferiore a 1/6.6lambda può essere definito a Diffrazione Limitata.
N.B. – E` comunemente asserito in molti testi astronomici che la Tolleranza Rayleigh di PV1/4lambda corrisponde a “Diffrazione Limitata” ma, come potete vedere dalla tabella, un semplice specchio senza ostruzione deve essere migliore. Preciseremo meglio di seguito la frequente associazione fra la definizione di “Diffrazione Limitata” con specchi da 1/4lambda.
E` bene notare a questo punto che la relazione esistente fra PV e le altre due misure, RMS & Strehl, dipende dal fatto che lo specchio sia relativamente liscio e privo da ogni significativa asimmetria.
Se uno specchio fosse quasi perfetto su quasi tutta la sua area, tranne su una piccola parte della sua superficie, allora sarebbe asimmetrico, avrebbe uno scarso valore PV, ma i suoi RMS e Strehl potrebbero sempre essere buoni. In questo caso, può uno specchio con alcuni valori inferiori a PV 1/6.6lambda ma con uno Strehl superiore a 0.93 essere definito a Diffrazione Limitata? – Tecnicamente dunque, il valore di Sthrel misura più accuratamente la qualità di uno specchio che il PV.
Ma se il valore di Strehl è più significativo, perché la Oldham Optical e la maggior parte dei produttori di specchi continuano a citare il PV come unità di riferimento per la qualità di uno specchio? – La risposta e`che il PV è la misura più semplice da rilevare e che, per un produttore di specchi professionale, è improbabile produrre specchi con una simmetria significativa! Perciò, la relazione fra PV e altre misure suggerita piu` sopra è generalmente un buon riferimento. Considerando inoltre che anche un appassionato con un po’ di esperienza può misurare il PV senza alcuno strumento sofisticato, questa è certamente una misura utile che un produttore di specchi può offrire.
Per quanto riguarda il PV 1/4lambda “Tolleranza Rayleigh”, Lord Rayleigh era uno dei maggiori esperti di ottica dell’epoca. Egli aveva capito cosa fosse possibile all’industria ottica del suo tempo, sapeva come funzionava la costruzione dei telescopi ed ebbe l’intuizione di quali difetti negli specchi avrevvero influenzato le performance delle ottiche.
Lo standard da lui proposto è però molto soggettivo. Quando lo introdusse egli era probabilmente consapevole che esso era ancora leggermente superiore al valore del disco di Airy, ma deve aver tenuto in considerazione i limiti dei telescopi dell’epoca. Così come l’effetto del rapporto d’ostruzione (di solito 20%?), i costi per produrre specchi a specifiche più elevate, la qualità degli oculari del tempo e le aspettative di cio` che – di fatto – si sarebbe potuto vedere attraverso ad un telescopio a quell’epoca. Alla fine sara` semplicemente giunto alla conclusione che uno specchio PV 1/4lambda (fronte d’onda), era lo standard economicamente piu` valido a cui mirare.
Lord Rayleigh propose questo standard più di 120 anni fa e, per molti utilizzatori di telescopi, esso è` ancora oggi un riferimento valido e preciso. La differenza fra uno specchio PV 1/4lambda e un PV 1/6.6lambda a “Diffrazione limitata” (o ancora migliore), non e` di fatto percettibile per la maggioranza delle persone che guardano attraverso un moderno telescopio.
Un produttore di specchi amatoriale che produce solo uno o due specchi nella sua carriera può considerare di aver fatto un ottimo lavoro se riesce ad ottenere uno specchio con un errore di fronte d’onda di 1/4lambda!
Non stupisce però che le tecniche ottiche siano migliorate negli ultimi 120 anni! Questo permette dunque ai produttori di specchi professionali di realizzare specchi con specifiche migliori di PV 1/4lambda nell’ambito degli specchi a diffrazione limitata e – in generale – a dei prezzi accessibili.
Oldham Optical e specchi a “Diffrazione Limitata” Pur avendo approfondito la definizione di “Diffrazione Limitata” e messo in evidenza come oltre a questo limite non riteniamo realistico mettere sul mercato specchi con il valore critico di 1/6.6lambda, in quanto esso è troppo vicino alla nostra gamma di specchi “Standard” a PV 1/4lambda (Fronte d’onda). Oldham Optical ha pertanto deciso di produrre e vendere la sua gamma di specchi a “Diffrazione Limitata” ad uno standard ancora più elevato, vale a dire PV1/10lambda (Fronte d’onda).
Perciò, da qui in avanti, quando ci riferiamo a specchi a “Diffrazione Limitata” di produzione di Oldham Optical, o anche in altre parti di questo sito web, – intendiamo PV1/10lambda (Fronte d’onda), RMS 1/30lambda o Strehl 0.96
RMS & Strehl Per tornare ai metodi di misura: l’errore superficiale RMS, come suggerisce il suo stesso nome, è calcolato facendo un certo numero di letture di errori diversi in varie zone della superficie. Per individuare singoli errori può essere utilizzata una lama “Null test” e, più letture si fanno, ovviamente, più accurato sarà il risultato finale.
RMS sta per “Root of the Mean Squares” (radice del quadrato medio). Gli errori rilevati vengono processati matematicamente, innanzi tutto ogni singolo errore viene elevato al quadrato poi, tali valori al quadrato vengono tutti sommati fra loro e la loro somma divisa per il numero dei campioni (questo determina la “media” dei valori). Infine, viene calcolata la radice quadrata del risultato.
(Il valore RMS puo` anche essere calcolato con sufficiente precisione direttamente dal valore di PV, assumendo che lo specchio si avvicini ad una curva nota o sia molto liscio)
Il “Rapporto Sthrel” o “Fattore Strehl”, è il rapporto fra la quantità di luce che, da una singola fonte puntiforme, cade all’interno dell’area del disco di Airy. Uno specchio perfetto avrebbe un valore di 1. Specchi non perfetti avrebbero valori inferiori a 1. In pratica, Strehl può essere calcolato con sufficiente precisione direttamente dal valore di RMS.
Dopo aver effettuato una serie di letture in diversi punti dello specchio o una lettura singola dell’errore PV con la conferma che lo specchio segua una certa curva o sia liscio, – potete calcolare il PV ed i valori corrispondenti in tutte le unita`.
Prima di abbandonare il tema dei rilievi qualitativi, – PV, RMS o Strehl – potreste essere interessati a sapere che non potrete mai far funzionare il Vostro telescopio con l’errore di fronte d’onda (sia PV che RMS) al suo valore minimo.
Cos’e` la prima cosa che fate quando guardate attraverso un telescopio?
Non muovete forse il fuocheggiatore avanti e indietro per mettere meglio a fuoco l’immagine?
Bene, quando fate questa operazione, state di fatto impostando il telescopio per il punto piu` piccolo che esso puo` ripordurre, – che con uno specchio a diffrazione limitata, significa che ogni punto di luce e` piu` piccolo del disco di Airy.
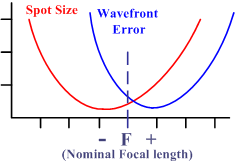
Molti di voi si sorprenderanno sapendo che, se fosse possibile misurare l’errore di fronte d’onda in questo punto, esso non sarebbe al suo valore minimo. Potendo sfocare leggermente l’immagine in una direzione, potreste arrivare a trovare la posizione dove l’errore di fronte d’onda è minimo, ma constaterete che il punto si è ingrandito ed è addirittura più grande del disco di Airy. L’immagine che vedreste attraverso il telescopio sarebbe perciò sfocata.
Dimensione minima del punto e minimo errore di fronte d’onda si escludono a vicenda, a meno che non abbiate uno specchio assolutamente perfetto… e vi abbiamo già ripetuto più volte che non ce ne sono !!!
Quindi, quando un produttore di specchi professionale cita l’errore di fronte d’onda PV, sta parlando dell’errore minimo che lo specchio puo` avere anche se, impostando il telescopio a tale punto l’immagine risulterebbe sfocata. Nonostante questo, l’errore risulta essere comunque un’utile misura per giudicare la qualità degli specchi.
Potrà inoltre sembrare strano che la superficie “fissa” di uno specchio possa dare origine ad un errore di fronte d’onda variabile??
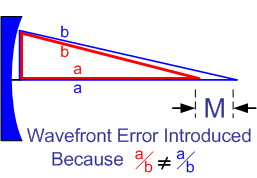
Ricordatevi che l’errore di fronte d’onda è misurato nel punto focale, dove voi state convogliando la luce da tutta la superficie dello specchio. Se vi allontanate dal punto focale anche solo di una piccola frazione di centimetro, allora le distanze fra la superficie dello specchio ed il suo asse e dalla superficie al bordo si modificheranno come i lati di un triangolo. Ogni distanza si modificherà in maniera diversa. La lunghezza d’onda e` di soli 0.000022″ perciò basta un piccolissimo movimento assiale vicino al punto focale per introdurre un grosso errore di fronte d’onda fra la luce che arriva lungo l’asse e quella che arriva invece dai bordi dello specchio. E` solo uno strano caso della vita che la posizione del punto più piccolo (migliore messa a fuoco), non coincide con la posizione del minimo errore di fronte d’onda.
Fiducia del cliente Molti dei nostri prodotti sono venduti a commercianti che possono testare gli specchi e che, grazie a questi test ed alla loro lunga esperienza, sanno che la Oldham Optical produce specchi secondo le specifiche richieste. Ma noi vendiamo anche a privati e, un grosso problema che un produttore di specchi come la Oldham Optical deve affrontare quando vende ai privati è quello di dimostrare loro che lo specchio in vendita rispetta le specifiche dichiarate.
Il tipico uilizzatore di telescopi di solito non ha l’attrezzatura necessaria o l’abilità per testare le specifiche di uno specchio. Deve fidarsi. Il problema della fiducia del cliente diventa più complesso quando, anziché essere venduti ad un cliente locale, gli specchi vengono venduti su Internet, spesso in paesi diversi.
Fortunatamente per noi, abbiamo un nutrito numero di venditori non stipendiati! – Molte delle nostre vendite provengono da persone che conoscono qualcun altro che ha uno specchio Oldham e ne è molto soddisfatto.
Approfittiamo di questa opportunità per ringraziare la vasta forza lavoro dei nostri lavoratori non stipendiati per i consigli, le raccomandazioni e la pubblicità gratuita che ci hanno fatto!
Uno specchio per telescopi non e` un oggetto economico, specialmente per dei privati. Noi ci raccomandiamo sempre che un cliente accorto faccia delle ricerche prima di comprare uno specchio, come ad esempio chiedere consiglio ai Circoli Astronomici locali o a gruppi di amatori e di consultare Internet prima di acquistare uno specchio.
Ma cos’altro può fare un costruttore di specchi per conquistare la fiducia del cliente? E` forse sufficiente affermare che lo specchio è conforme alle specifiche e lasciare che il cliente lo accetti sulla base della fiducia?
Nel caso di piccoli specchi, – tutto sommato economici, – per i quali la fornitura di test e certificati rappresenterebbe una parte importante della spesa, forse è possibile “fidarsi” Ma quando si parla di una considerevole somma di denaro lo riterreste sempre opportuno?
Chi compra uno specchio di solito preferisce ha più fiducia se può avere qualche prova qualificata a conferma delle affermazioni del produttore. Per tutti gli specchi da 20” in su, Oldham Optical fornisce sempre un certificato di conformità (senza spese extra), mentre per gli specchi più piccoli offre lo stesso servizio a pagamento.
Siamo stati estremamente sorpresi nel constatatare quanti clienti richiedono i certificati di conformità anche per i piccoli specchi per i quali dovevano pagare!
Per spiegazioni più approfondite, vogliate far riferimento alle pagine del sito dedicate ai “Test”.
Allora? – Siamo riusciti ad individuare uno standard soddisfacente per uno specchio? Come affermato, esiste già uno standard soddisfacente per uno specchio che può soddisfare la maggior parte degli operatori; si tratta della “Tolleranza di Rayleigh”, vale a dire errore di fronte d’onda PV 1/4lambda, (errore di superficie PV 1/8lambda), espresso anche come RMS 1/15lambda o Strehl 0.82. Per coloro che possono permettersi di pagare di più, uno standard molto soddisfacente nell’ambito degli specchi a “Diffrazione Limitata” è offerto da un errore di fronte d’onda PV 1/10lambda (errore di superficie PV 1/20lambda), che può anche essere espresso come RMS 1/30lambda o Strehl 0.96.
Oltre questo limite non sono possibili ulteriori significativi miglioramenti.
Spiacenti! – Non e` tutto qua! Abbiamo affermato precedentemente che uno specchio a diffrazione limitata si comporterà con le stelle esattamente come uno specchio perfetto ma, se vi ricordate, avevamo espresso una riserva riguardo a questa affermazione per quanto riguarda l’osservazione della luna e dei pianeti. C’è un altro fattore di cui bisogna essere consapevoli quando si progetta un telescopio, tale fattore riguarda le ostruzioni ed i confronti fra le performance di telescopi riflettori e rifrattori.
Un altro parametro poco noto usato per giudicare la performance di uno specchio è il “Fattore di Contrasto Su altre pubblicazioni e` noto anche come “Rapporto di Contrasto” e molte altre combinazioni di questi termini. Nel nostro sito abbiamo deciso di definirlo Fattore di Contrasto (Contrast Transfer Factor) o CTF.
Benché possa essere utilizzato per definire le caratteristiche di un singolo specchio isolato, esso è molto più utile quando viene utilizzato per valutare dei sistemi – specialmente con ostruzioni – come ad esempio i telescopi Newtoniani o Cassegrain.
L’effetto delle ostruzioni ed il metodo per calcolare il valore di ostruzione sono affrontati nella sezione del sito riguardante i disegni.
Praticamente CTF è la misura di quanto “Bianco e Nero” si trasforma in “Sfumature di Grigio!”
Immaginate una sequenza di linee bianche e nere. Man mano che le linee si assottigliano e si avvicinano le une alle altre, si giungerà ad un punto in cui esse incominceranno a confondersi e a sfumare nel grigio. Se portato al limite, le linee bianche e nere si fonderanno in un’unica sfumatura di grigio medio.

Di solito il CTF viene espresso come un grafico di percentuali o sotto forma di frazioni che rappresentano il numero di “linee per mm”. Qui di seguito potete vedere ad esempio uno specchio 10″ F/5.
Con uno specchio a diffrazione limitata tale limite si trova dove le linee si avvicinano al diametro del disco di Airy. Per un 10″ F/5, esso è di circa 355 linee/mm e, nel grafico, esso si trova nel lato destro, nel punto in cui le linee bianche e quelle nere sfumano completamente in un colore grigio medio.
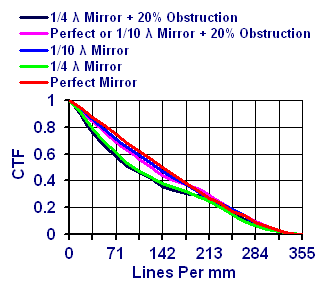
E’ possibile disegnare nel grafico linee singole per indicare gli aggiustamenti di ogni “sistema” e confrontare specchi con errori PV 1/10lambda e 1/4lambda di fronte d’onda con uno specchio perfetto.
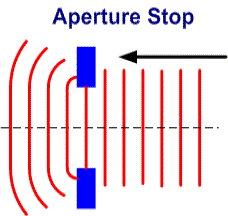
Il problema con i sistemi Newtoniani o i Cassegrain è che il secondario ellittico o piano rappresentano delle ostruzioni alla luce in entrata e, poiché le ostruzioni creano ulteriori effetti di diffrazione, il risultato finale è quello di ridurre il CTF dell’intero sistema.
Un tipico Newtoniano puo` avere un rapporto d’ostruzione di circa 20%, come indicato nel grafico:-
Notate tre punti importanti relativi al grafico:
- Uno specchio 1/10lambda con un’ostruzione del 20% si comporta esattamente come uno specchio perfetto con la stessa ostruzione del 20%, – non c’è nessun significativo vantaggio ad avere uno specchio migliore di 1/10lambda.
- Uno specchio da 1/4lambda senza ostruzione non è migliore di uno specchio da 1/4lambda con un’ostruzione del 20%, – perciò telescopi con specchi da 1/4lambda possono avere ostruzioni fino al 20% senza che questi vada a deteriorare significativamente l’immagine.
- Viceversa, se state pianificando di avere un rapporto di ostruzione inferiore al 20%, – allora, per beneficiare di tale rapporto d’ostruzione inferiore, c’è bisogno di uno specchio migliore di 1/4lambda. Dovreste prendere dunque in considerazione uno specchio da 1/10lambda.
Un secondo fattore è quello che può in parte spiegare il motivo per cui si associa sovente il termine “a diffrazione limitata” con gli specchi da 1/4lambda. Se dovete avere un’ostruzione del 20%, che è un valore tipico per un telescopio Newtoniano, allora uno specchio da 1/4lambda rappresenta il limite in cui il “sistema” può essere definito a “Diffrazione limitata”. In questo caso significa che la qualità dello specchio migliora davvero di poco oltre a 1/4lambda e, quando ha proposto 1/4lambda come tolleranza (Rayleigh Tolerance), Lord Rayleigh doveva essersene ben reso conto.
(Quando usa la definizione a “Diffrazione Limitata” Oldham Optical si riferisce sempre a 1/10lambda, (o Strehl 0.96), come precedentemente illustrato)
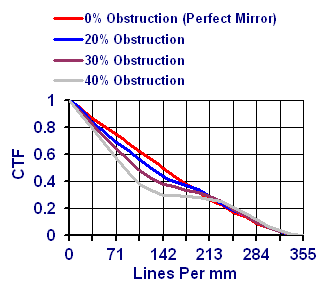
Rapporti di ostruzione superiori a 20% hanno progressivamente effetti più evidenti. Nel secondo grafico potete vedere l’effetto di una crescente ostruzione. In questo caso i grafici si basano tutti su uno specchio perfetto (o a “Diffrazione Limitata”) da 10” F/5.
L’effetto concreto di tutto ciò è che, se state vedendo la luna o i pianeti con un telescopio con un’elevato rapporto di ostruzione focale, come per esempio piu` del 25%, – allora ci sarà una progressiva perdita di contrasto che andrà a discapito dei piccoli dettagli. Questo non avverrà invece quando si guardano le stelle in quanto esse hanno un contrasto cosi` forte che anche con bassi CTF di <0.1 non ci sono effetti evidenti.
I Cassegrains di solito hanno rapporti d’ostruzione del 30-40% ma, prima che li condanniate come telescopi mediocri, – non dimenticatevi di altri vantaggi quali, un maggiore ingrandimento e campi più grandi che, a parità di dimensioni, i Newtoniani non possono offrire. Ricordatevi che, quando si progetta un telescopio bisogna sempre accettare qualche compromesso.
Tutto ciò conferma quanto affermato nella pagina relativa ai disegni di questo stesso sito, se state progettando un telescopio per osservare la luna o i pianeti, allora dovreste cercare di tenere il rapporto di ostruzione piu` basso possibile, compatibilmente con il campo visivo che desiderate ottenere.
Per quanto riguarda il CTF, di sicuro un telescopio rifrattore, è migliore di un riflettore per l’osservazione della luna o dei pianeti in quanto non ha ostruzione. Infatti, se per l’osservazione della luna e dei pianeti un buon rifrattore da 6″ può battere un buon riflettore da 6″, – il potere di concentrare la luce di un riflettore da 8″, è sufficiente per uguagliare la performance di un rifrattore da 6″ e, specchi riflettori più grandi -come un 10″- possono facilmente batterlo. Per quanto riguarda dunque il CTF, in questa serie di grandezze aggiungendo 2″ al diametro di un riflettore si ottengono performance equivalenti ad un rifrattore.
Oltre ai 6″ di diametro i Rifrattori diventano estremamente costosi al punto da diventare impraticabili. Per la visione di luna e pianeti un buon rifrattore da 24″ potrebbe sicuramente battere un buon Newtoniano da 24″ – ma costerebbe una fortuna produrlo e non entrerebbe mai nel baule della macchina!
Conclusioni? Le conclusioni che potreste trarre da questa pagina possono essere:-
- Specchi con errore di fronte d’onda PV 1/4lambda sono molto soddisfacenti per la maggior parte degli utilizzatori ed hanno un prezzo ragionevole.
- Specchi con errore di fronte d’onda PV 1/10lambda offrono un leggero miglioramento rispetto a 1/4lambda, ma ad un prezzo superiore.
- E` quasi inutile cercare di andare oltre a 1/10lambda, in quanto non ci sarebbe un miglioramento significativo.
- Se state disegnando un telescopio per l’osservazione della luna e dei pianeti tenete il rapporto d’ostruzione il più basso possibile.
- Se state considerando un’ostruzione inferiore al 20%, sarebbe meglio usare uno specchio da 1/10lambda
Ed infine Una nota finale per gli appassionati che vogliono levigare e lucidare i propri specchi: è assolutamente possibile per voi produrre uno specchio da 1/4lambda a casa vostra – anche se consumerà molto del vostro tempo e tutto il vostro impegno! Se ci riuscite, avrete tutte le nostre congratulazioni per aver ottenuto tale standard (se riuscite a fare un 1/10lambda a casa vostra – magari potreste darci un colpo di telefono per avere dei dettagli sulle assunzioni!)
Il primo specchio prodotto da Norman Oldham, quando l’Astronomia era ancora un hobby e non un business, era un 6″ F/10. Ci vollero 6 mesi per produrlo e Norman afferma che fosse a diffrazione limitata! – per qualche ragione comunque esso sembra essere scomparso dopo l’ultimo trasloco del laboratiorio?