It can be extremely surprising and annoying to find out that the big parabolic mirror you have just paid a lot of money for cannot focus all the incoming light down to an infinitesimally small point, but instead puts it into a finite sized disc with some faint rings around it.
You have been told the Airy Disc cannot be avoided and that it’s due to diffraction and the wave nature of light, but every explanation you look up soon disappears off into the deeper realms of mathematics. It all seems a bit of a fiddle!
Well – I am afraid a lot of the mathematics cannot be avoided if you need to go into the subject deeply, but it is possible to get a working knowledge of what’s happening without too much of the maths and with just a bit of thinking in the bath and a bit of work on the kitchen table with a ruler and compass.
Perhaps the easiest way to start to visualise what’s happening with your parabolic mirror is by considering the wavefronts of light coming in from a distant star. The star is so far away that the light rays approaching can be considered parallel, and the approaching wavefronts can be considered flat plane lines, across the incoming parallel rays.
If you live at the seaside, stop and look at a series of waves marching in towards the beach. If the tide is well up and they hit a concrete sea wall, – you will often see them reflect back. If the sea wall happens to be curved, you may even see some of the reflected waves converge, (focus), towards a point.
The Airy Disc –
An Explanation of What it is and Why You Can’t Avoid it

Unfortunately, not many sea walls are designed with the perfect parabolic shape to be an example of how a parabolic mirror works but any concave curve should show some focussing effect, enough for you to get an idea of what’s happening.
(Don’t lean over the railings too far and if anyone starts looking at you strangely – its probably time to move on and get an ice cream!)
So getting back to light and a parabolic mirror – The flat wavefronts march in to the mirror like waves in the sea and are reflected. The parabolic shape of the mirror converts the incoming flat wavefronts into reflected spherical wavefronts. These spherical wavefronts converge at the focal point of the mirror. See the diagram below.
If the mirror was perfect, light was not comprised of waves and diffraction did not exist, the focal point where all the light converged would be infinitesimally small.
Sorry! – It’s just not like that

Diffraction is something that happens at edges. When something like light meets the edge of a solid object, some of the energy tries to bend round it.
The usual diagram seen in Physics textbooks to illustrate Diffraction is of flat wavefronts approaching a screen with holes in it. The holes are small and close to the wavelength of the light used. The light passes through the holes and then part of it tries to bend around the edges of the holes as it emerges.
If the holes are small and not many wavelengths of light wide, then the resulting wavefront from each is spherical. It appears as if the light is being generated from point sources situated at the holes themselves, rather than the actual source which is somewhere behind the screen
The really interesting thing is where you have two or more holes all acting as point sources, the light from each hole will interfere with each other. That is what happens with a Parabolic mirror to form the Airy Disc and the rings.
There is an experiment you can do in the bathroom at home that illustrates the same wave effect, but note this health warning first – it might not be a good idea to let your wife find out you are carrying out experiments of this nature!
So sneak into the bathroom armed with blocks of wood and float them in the bath. They should be spaced with a small gap between them. Make waves on one side and watch how they propagate through the hole.
If you don’t think you dare try this in the bath, you can do the same thing just as well in the garden pond with a couple of rocks, but do not let the neighbours see you! They might tell the wife!

In real life, the reflected light from the edge of the mirror merges with the rest of the wavefront reflecting from the main surface of the mirror.
Most of the combined wavefront is spherical from the main body of the mirror but bends back in the opposite direction towards the edges.
It is the departures at the edges that form the rings around the central Airy Disc.
Although it sounds very complicated, its actually very simple to demonstrate what is happening just by sitting down at the kitchen table and drawing out the wavefronts on a piece of paper and a compass.

Start by drawing a mirror say 2 “ in diameter. Then with a compass you are going to draw out concentric arcs from each rim of the mirror to represent the wavefronts as in the diagram adjacent. Each arc must be regularly spaced as it represents a wavelength
So draw say 10 arcs from each rim of the mirror starting at say 2″ radius, and at every ½” out to say 7½”. The arcs from each rim will intersect.
If these pencil arcs were waves of light they would interfere with each other. Where two arcs cross there would be a bright patch of light and where one arc is half way between two other arcs from the second rim, they would cancel out and give a dark patch.
If you then look at what you have drawn you will see you can draw a series of straight lines through the intersections. All lines begin from roughly the centre of the mirror. These lines represent the bright patches of light.
They are the black dotted lines in the diagram, with the central bright spot shown in a heavy black line.
Now steadily go through the drawing and put a mark where one line from one rim is half way between two lines from the other rim. Once finished the marks should lie on a second series of lines that again start at roughly the centre of the mirror and run out through the marks. This series of lines is the dark patches that exist between the Airy cisk and the rings.
The first two defining the Airy Disc are the blue dotted lines in the diagram.

Although on flat plain paper these are drawn as lines, on a three dimensional parabolic mirror they represent cones of light. Where these cones intersect the focal plane of your telescope they will appear as a bright central disc with rings around it.
The central disc is of course the Airy Disc. In practice, when looking through a telescope the rings rapidly get faint and it is usually only the first ring and perhaps the second that can be seen in practice.
The angle of the disc and of the first ring is illustrated on the diagram above. The first Airy Ring is easy to work out. It is the first set of bright intersections away from the central spot. The Airy Disc itself is not quite as easy to see at first.
The accepted convention for the size of the Airy Disc is to measure to the centre of the first dark patches either side of the central spot. The diagram should give you the lead.
Instead of using the term “angle to the disc”, the term more commonly used in astronomical circles is “angular diameter”. So please note that when the rest of this document uses “angular diameter”, it means the angle to the Airy Disc (or rings), as described above.
If you repeat the drawing with different diameter mirrors, say 1” and 3”, while still using ½” rings to represent the same wavelength, you will find that as you increase the diameter of the mirror, the angular diameters of the disc and the ring reduce. Since the angular diameter reduces, the physical diameter of the disc and rings also reduce.
Although this illustration is just something done on the kitchen table, It is exactly the same mathematics that apply with light to form the real Airy disc and Rings. The angular diameter of the disc and rings is calculated with exactly the same rules. It follows that the Airy Disc gets smaller as the diameter of the mirror increases.
Before the people who really understand mathematics jump in and complain that the intersections are not really on straight lines, they are on hyperbolic curves, it is agreed that they really are on slight curves rather than straight lines! The lines come in from infinity and do bend very slightly as they approach the mirror. So evidence of a slight curve is likely to be noticed on the kitchen table using wavelengths of ½” with a 2″ mirror.
However light has a wavelength of about 500nM, so the line for the first Airy Ring will have come in from infinity and will bend out of line near the mirror a maximum of ½ a wavelength, which is about 250nM. It is submitted that coming all the way from infinity and only bending 250nM out of line is still pretty damn straight!
In any case, the accepted formulas used for working out Airy Disc size and angular diameter assume the lines are straight, so no reason this description cannot be allowed to do the same!
The description above only covers light from the rim of the mirror – so what about the light from the rest of the mirror? Don’t forget the rest of the mirror surface is pouring light into the central spot. The very simple explanation is that this light merges with the light scattered from the rim of the mirror to give the bright Airy Disc.ù
The only practical thing a telescope constructor can do to make the Airy Disc smaller is to make the mirror diameter larger. This makes the angular diameter of the Airy Disc smaller. The angle is fixed for any one diameter of mirror. Once the angle is fixed, the physical size of the Airy Disc is determined solely by the focal length of the mirror.
A common formula used for working out the size of the Airy disc uses the Focal ratio, which includes both the diameter of the mirror and the focal length in one term.
One formula for the Airy Disc is:
- D = 2.43932 x λ x Focal Ratio
- D = Diameter of Airy Disk in mm
- λ = Wave Length in mm (e.g. 546nM = 0.000546mm)
- (If Focal ratio = F/4 & 546nM used then D = 0.00533mm)
- One formula for the diameter of the Airy Disc is:
- A = 7200(Arc Tan(1.21966 x λ /d))
- A = Angular Diameter of the Airy Disk in Arc Seconds
- d = Diameter of Mirror in mm
Ok! So you now know what the Airy Disc is! But from the description above you should be thinking there’s a easy way to get rid of the thing!
Surely if it’s just the light at the edge of the mirror that causes diffraction, then why not just mask off the edge of the mirror with a cardboard ring? This will stop light hitting the edge of the mirror. Wont this get rid of the Airy Disc?
Sorry – this does not work! You now get diffraction from the edge of the mask instead! What you have done by masking the mirror edge is add what is called an “Aperture Stop” to your optical system.
By doing so you slightly raise the focal ratio of the equation and the Airy Disc actually gets bigger.
This also explains why in your telescope you need to keep the spider holding the elliptical flat or secondary mirror as small and unobtrusive as practical. Any obstruction causes additional diffraction.
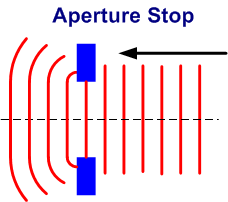

Finally, – here is the killer – let’s suppose you could magically mask off the edge of the mirror without causing extra diffraction. You have managed to limit the beam of light falling on the mirror to less than the mirror diameter so the edge of the mirror is not illuminated. You must really think you have the problem cracked now?
Sorry – This still does not work! The edge of the beam of light falling on the mirror surface is itself a discontinuity. When it strikes the mirror and reflects it behaves exactly as if it was a real physical edge.
There is diffraction from the edge of the beam exactly the same as if it was the physical rim of the mirror. For this situation there is no easy and simple “kitchen sink” explanation. This is where I “cop out” and say this is due to the wave nature of light and you do need to start digging into the physics text books if you want to understand it better.
Exactly the same thing happens if you paint the outer edge of your mirror with black paint. All this does is cause diffraction to occur where the black paint finishes and the reflective surface starts. All you have done with the paint is reduce the diameter of the mirror. The result is that the Airy Disc gets bigger.
The message is that you cannot avoid the Airy Disc.
However you can make it smaller: You can either increase the diameter of the mirror, which reduces the angular diameter of the Airy Disc, or reduce the focal length of the mirror, which reduces the physical size of the Airy Disc.
The Airy disc size is suddenly becoming more important to amateur astronomers due to the recent improvements in digital cameras where the CCD sensor pixel size has now reduced to the point where it is comparable or smaller than the Airy Disc size. In future, telescope mirror diameter and focal length may have to be chosen to better match the CCD pixel size?
To close, it is possible you could completely avoid the Airy Disc by using an infinitely large mirror – but I would respectfully suggest a long talk with your wife or perhaps your doctor before trying to order one of these.